【第二法則を確かめよう】
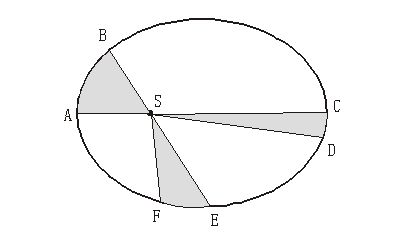
第2法則は火星がA→B,C→D,E→Fを通過する時間がすべて等しいなら
= = となる。
実際はどうだろうか,以下の手順で確かめる。
① M1→M2の日数を計算する。
日
M3→M4の日数を計算する。
日
M5→M6の日数を計算する。
日
② グラフの方眼を利用して以下の面積を求める。
扇形M1SM2の面積=方眼 個
扇形M3SM4の面積=方眼 個
扇形M5SM6の面積=方眼 個
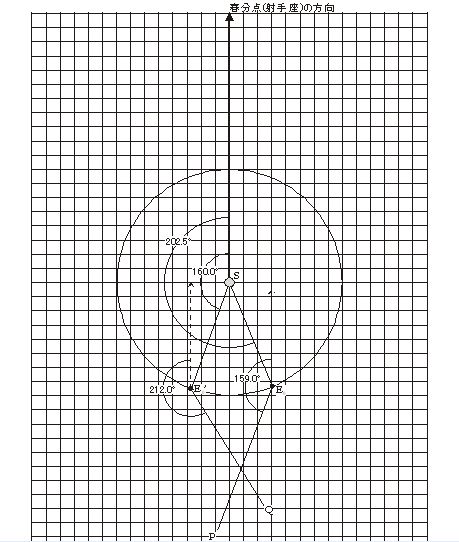
723.ケプラーの法則の発見を追体験しよう <ワークシート> (1)ケプラーの法則とは 【歴史的な背景】 ①コペルニクスによる地動説(「天体の回転について」1543年)後も、すぐには受け入れら れなかった。 ②ケプラーの時代(ヨハネス・ケプラー、1571~1630)はまだ天動説と地動説がせめぎ合っ ていた。 ブルーノが火炙りの刑(1600年)、ガリレオの裁判(1633年。地動説を捨てることを条件に 減刑。ガリレオの無罪と名誉挽回は1992年、ヨハネ・パウロ2世によるまで、約350年も要し た。)など、この時代は地動説を主張するには危険をともなった。 ③ティコ=ブラーエ(1546~1601)は当時としては極めて正確な観測をおこなった。(精度5 秒を追求)その精度をもってしても年周視差は見つけられず、かえって天動説を補強する結果 となった。しかし、同時に正確なデータは惑星の運動が等速円運動をしていないことを示して いた。(年周視差はもっと観測精度が必要であった。) ④ケプラーはティコのこれらのデータを使って惑星(火星)についての法則を見つけた。 ⑤等速ではない・・・太陽の近くで速く、遠ざかると遅い・・・面積速度が一定となるような 動き・・・第二法則の発見。 最初の発見は、第二法則(面積速度一定の法則、1609年) 法則の名前順ではないことに注意。 その後に第一法則(楕円軌道、1609年)を発見している。 ⑥ケプラーとティコ=ブラーエとの関係は謎が多い。 ⑦楕円であることはケプラーにとってショック。 (ケプラーは、「宇宙は神によって幾何学的に支配されている」と考えていたため) ⑧第三法則(調和の法則、1619年)は難儀した。公転周期の2乗が公転半径の3乗に比例する ことを見つけるには第二、第一法則の発見から、なお10年以上の歳月を要し、70回以上の検 算を行ったという。桁数の大きい数値データからこの法則を見つけるのはケプラーの執念とし か言いようがない。ケプラーの時代はまだ対数の概念がなく、対数表を使えば割と簡単に発見 できたかもしれない。(対数は1614年にイギリスで発明されるが、プラハで出版されたのは 1620年のことで間に合わなかった) とにかくケプラーの法則は、経験則として見いだされたものだということ。理論的な解明は後 にニュートンの万有引力の法則でなされた。 (2)実習の資料について ①グラフ用紙のSが太陽,Sを中心とする半径4cmの円は地球の軌道です。 資料のイとロのデータを記入した図があります。これより火星の位置をもとめます。 同様なことを数多くとれば火星の軌道が求められるというわけです。一通りやるには20年くら いのデータが必要となります。 ②1965年4月13日の夜,地球は,春分点の方向とSE0のなす角=202.5°であるE0の位置にありま す。(この角度を日心黄経といいます) そのとき火星が春分点の方向となす角度=159.0°の方向にあることが観測されました。 (この角度を地心黄経といいます)このデータより,直線E0Pを引く。火星は直線E0Pのどこか に存在します。 ③火星の公転周期)は1.88年(687日)であることがわかっています。これより,火星は1967年3月 1日に元の位置に戻ってきます。そのとき地球は,春分点の方向とSE0’なす角=160.0°である 0’の位置にあります。そのとき火星が春分点の方向となす角度=212.0°の方向にあることが観 測されました。 このデータより,直線E0Qを引くと、火星は直線E0Qのどこかに存在するはずです。 ④この2つの日には同じ場所にいる火星を観測しているわけですから,その火星の位置とはE0P とE0Qの交点になります。こうしてM0が決まりました。 (3)火星軌道の作図の手順 ①M0を記入します。 ②表1の地球・火星のデータからM0と同様にM1~M7の位置を求めます。 ③これらの8点をなめらかな曲線で結んで,火星の軌道を作図します。
【火星軌道決定資料1】(表1)
|
年 月 日 |
地球の位置 |
地球と春分点の なす角度 (日心黄経L) |
火星と春分点の なす角度 (地心黄経λ) |
火星の位置 |
|
イ、1965. 4.13 |
E0 |
202.5° |
159.0° |
M0 |
|
ロ、1967. 3. 1 |
E0’ |
160.0° |
212.0° |
|
|
1967. 6. 2 |
E1 |
251.0° |
196.0° |
M1 |
|
1969. 4.19 |
E1’ |
208.5° |
256.5° |
|
|
1969. 7.21 |
E2 |
297.5° |
243.0° |
M2 |
|
1971. 6. 8 |
E2’ |
256.5° |
316.0° |
|
|
1971. 9. 9 |
E3 |
345.5° |
313.0° |
M3 |
|
1973. 7.27 |
E3’ |
303.5° |
22.0° |
|
|
1973.10.28 |
E4 |
34.0° |
30.5° |
M4 |
|
1975. 9.15 |
E4’ |
351.5° |
77.5° |
|
|
1975.12.17 |
E5 |
84.5° |
82.5° |
M5 |
|
1977.11. 3 |
E5’ |
40.0° |
123.0° |
|
|
1978. 2. 4 |
E6 |
134.5° |
118.0° |
M6 |
|
1979.12.23 |
E6’ |
90.5° |
162.5° |
|
|
1980. 3.25 |
E7 |
184.0° |
146.5° |
M7 |
|
1982. 2.10 |
E7’ |
140.5° |
199.0° |
【実習】第一法則を確かめてみよう。 【楕円の特徴】 ①楕円の一番長い直径上に焦点が2つあり,楕円上の任意の点と2つの焦点の距離の和はすべて等しくなる。 図でいうと = =
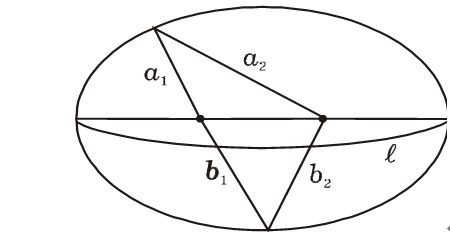
これが火星の軌道に当てはまるか以下の手順で確かめる。 ②一番長い直径を探し,直線を引く。 ③太陽Sと対称な位置にもう一つの焦点S’を記入する。 ④物差しで以下の長さを測定する。 SM2+S'M2= cm SM4+S'M4= cm SM7+S'M7= cm
【作図】資料1のデータを用いて記入してみよう。

【第二法則を確かめよう】

第2法則は火星がA→B,C→D,E→Fを通過する時間がすべて等しいなら
= = となる。
実際はどうだろうか,以下の手順で確かめる。
① M1→M2の日数を計算する。
日
M3→M4の日数を計算する。
日
M5→M6の日数を計算する。
日
② グラフの方眼を利用して以下の面積を求める。
扇形M1SM2の面積=方眼 個
扇形M3SM4の面積=方眼 個
扇形M5SM6の面積=方眼 個