軸周りのモーメントは、次のように考えると正解にたどりつけます。 右側のおもりの腕の長さは、回転したとしても　L　に固定されています。 一方、左のおもりは、回転すると 「回転中心」から、「おもりにかかる重力の方向」への垂線の長さが変わります。 ここで左右のバランスがとれるためには、左のおもりの「腕の長さ」（＝モーメントの計算に用いる長さ）は 4L　になるはずです。 　　(左）　4L * m = L * 4m　(右） なので、答えは　イ　　でした。 （実験器具も　イ　の形を示しています！） 全てまとめた動画はこちら 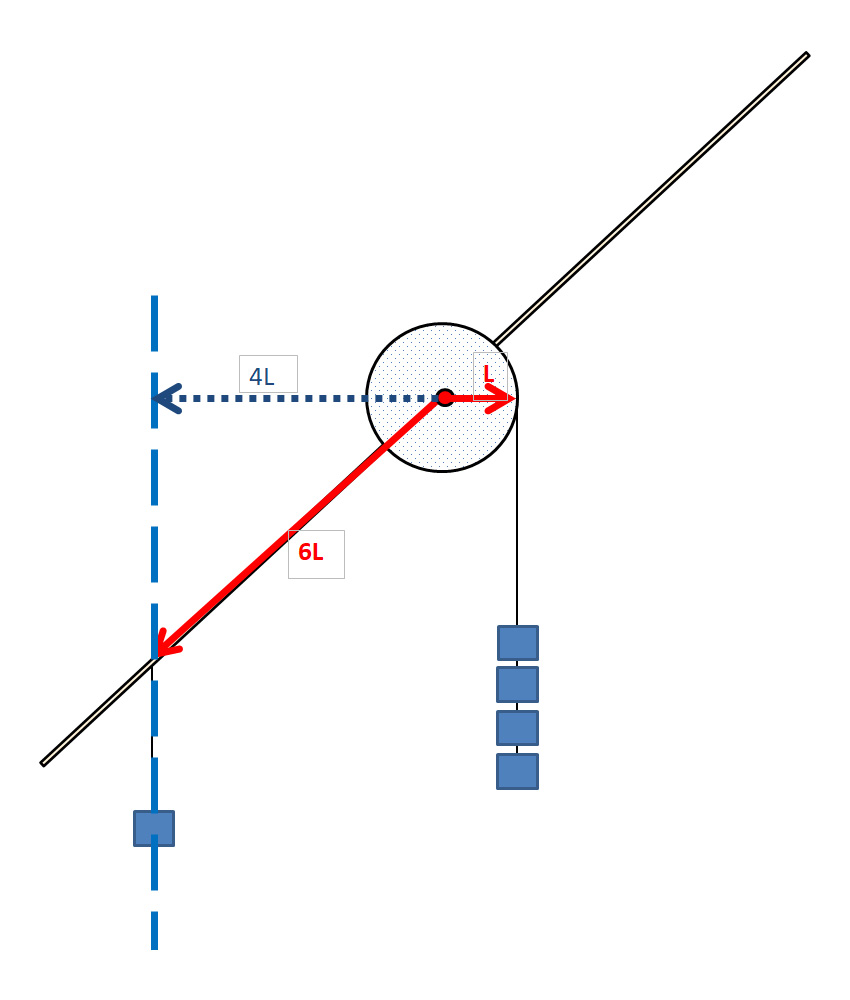これは、6L　であろうが、8L　であろうが、事情は同じです。 なので、以下の図のようになるとバランスがとれます。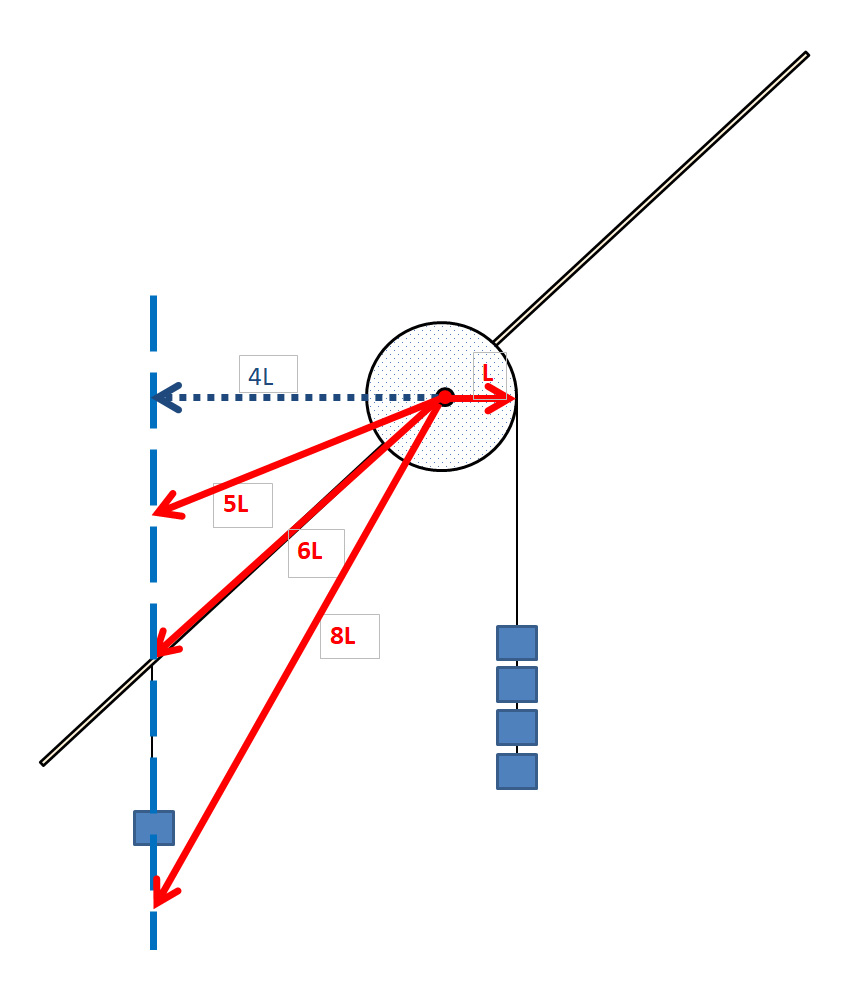